

Last Updated on August 3, 2023 by user
Geometry is the branch of mathematics concerned with the properties and relations of points, lines, surfaces, solids and higher dimensional analogs. For many students, this proves to be a barrier to math success, and they will often turn to you, the parent, for geometry help.
But this can create its own problems. Even if you excelled at geometry and math as a student, it’s likely been a while since you have practiced it, and you may not be able to explain it in the way your student was taught in school.
Don’t worry if you don’t have directed tutoring experience or even remember anything from your math class- that’s why we have put together this guide for you so that you can teach geometry proofs to your student as a private math tutor or teacher would. It will also help improve your child’s study skills in terms of how to layout proofs according to what the teacher deems necessary.
Taking your student to a specialized math center for a session with a private tutor may not be convenient or available in your area. That’s when you have to take matters into your own hands despite not having any direct tutoring experience.
For some students, their problem with understanding geometry could be inherent in their nature. There is some evidence to suggest
that people tend to either relate to math in a more numbers-driven, arithmetical way or a visual/geometric way.
For those in the first group, reasoning spatially is not as easy as it is for the second group, which makes it harder to learn geometric concepts. But don’t give up; math skills can quickly be learned and developed over time!
One of the most common of all geometry problems is the two-column proof.
Two-column proofs are dreaded by many students as they require them to not only give factual statements to answer the proof but also require students to provide a reason for every statement that is given.
This added step takes extra time and can be frustrating for many students.
These five steps are based on this video by Rick Scarfi.
In the video, Scarfi breaks down what is needed to complete and master two-column proofs. With these tips, you’ll be able to provide a great tutoring session and geometry help to your student whether it’s with homework or test prep.
The postulates, theorems, definitions, and properties of geometry are very important for solving two-column proofs. This is where the statements and reasons come from, and your student needs to have a solid knowledge of these – or know where they can find them – to solve geometry problems if they don’t have access to online math tutoring.
These should all be available in your student’s geometry textbook they will be toting with them for homework. It can also be useful to create a reference sheet to use when working on these types of problems. The more of these that your student has mastered, the quicker they can solve proofs without having to review their reference sheet.
Geometry problems are typically visual, and going the extra step to label the drawing that has been provided is key to solving them. If you do not have a drawing, it is recommended that your student draw a picture of what is given for a visual example to review while working through the proof.
Your student will use the given statement to label the pieces of the drawing that are being considered. For example, if the statement indicates that two lines are parallel, your student may want to draw over them or highlight them to get a better visual representation of the problem they are solving. You may also suggest that they mark the midpoint of a line inside the drawing with an “m” or another indicator, so the center is visually clear as well. This is just one of the tips that an experienced tutor employs.
“The picture is a visual to help you to think through the proof,” Scarfi says. It’s all a part of learning.
Your student can continue labeling as he/she works through the various steps of each proof. Remember: labeling should not be limited to just the beginning of the problem.
In this example below, you can see that Scarfi labeled the parallel lines AS and TB, congruent angles 5 and 2 and then 6 and 1, the midpoint at O and congruent sides AO and OB.
When completed, proofs will often look messy – and this is a good thing! Sometimes, labeling in the later steps can lead your student to the full answer, as they can literally see where the statements are leading them.
Geometry proofs are interesting as they tell your student what they need to prove. Your student just has to figure out how it is proven.
It may seem obvious, but knowing what is it that you are trying to prove is the key to solving any proof problem. For example, what the problem is asking your student to prove might not have any of the same numbers as having been given in the visual elements of the problem.
You can see this in the following example, as angle 7 is not stated in the given.
This tells your child that, at some point, while he or she is attempting to provide a solution, they will have to provide a statement – and corresponding reason – that lets them use this number.
Another teaching tip, Scarfi suggests writing out what you are proving (again) underneath the columns to give your student clear direction as they take on the geometry problem. Knowing what they are trying to prove can help your student narrow down postulates, theorems, definitions, and properties to the ones that will be most helpful in solving the problem.
After getting them narrowed to a few of the most appropriate ones, your student has fewer variables to work with, and then they can focus on determining which answer is the right one.
It’s important to fill out the given information first when solving proofs. Sometimes an obvious step is overlooked as a given, so be sure to go over all of these first.
If your student is at the level of creating their own statements (rather than having them provided by the teacher), they’ll typically want to put the “given statements” in the first step.
It’s also important to remember that the “given statements” are provided on purpose to help your student decide the best way to prove what has already been established. The “given statement” is there to tip you off to the other theorems, postulates, properties, and definitions that are true for this problem so that you can use these to solve the proof.
Sometimes, what you are trying to prove in a geometry proof falls outside of the knowledge you can gather from the statements that have been given. By knowing the theorems, postulates, properties, and definitions, your student can introduce their own additional givens based on what they already know.
For example, the “given statement” below does not mention angle 7, which your student is trying to prove.
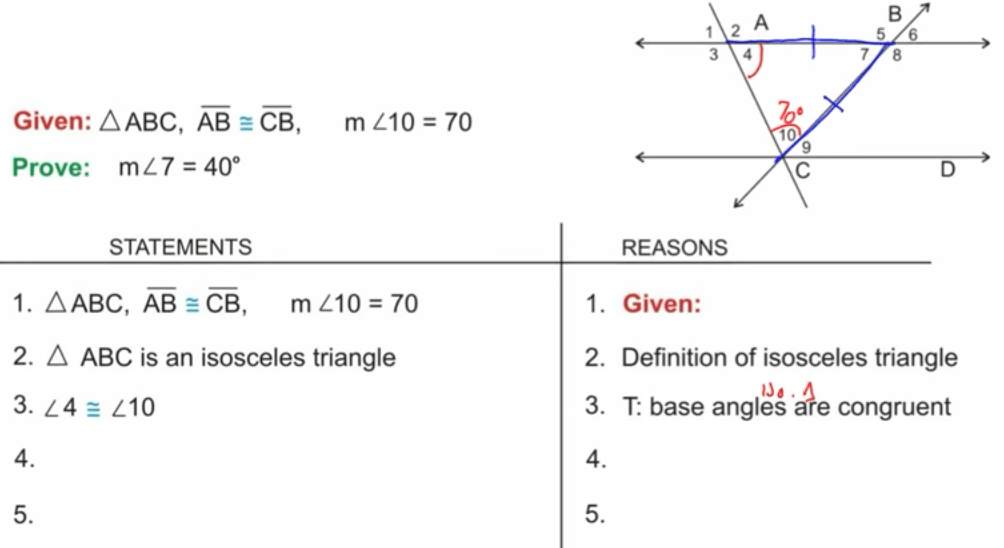
But, if the “given statement” helps your student figure out that the triangle is an isosceles triangle, your student can then use what they know about the definition of an isosceles triangle and its angles to figure out the third angle (See step 4 in the example below) and move to the next step.
This is a great example of using a strong math foundation to solve new problems – a skill we often encourage here at Thinkster!
Sometimes a mathematics course teacher or the teaching assistant wants to make sure that the statements within the proof solution are symmetrical.
In the example below, the “given statement” shown in step 1 has SA (from triangle SOA) on the left and TB (from triangle TOB) on the right, but what is being proven has them reversed. If your teacher is very technical, they may want your student to use a symmetric property to switch them around to match what is being proven – shown in step 5.

It’s also important to write out the reasons in the way that your student’s teacher prefers. The teacher may want everything written out in the long form or he or she may want your child to use specific symbols and abbreviations.
In this same vein, you don’t want to end your proof too early.
You may have been able to prove the first or second aspects of the proof, but many teachers will want their students to show all of the statements and reasons they can use to complete the proof.
For example, to prove that two triangles are congruent, your student may have already been able to show that two of the angles within each triangle are congruent and two sides are equal in length. These are shown in steps 2 and 3 below.

It may be important to take this one step further and actually write out that the sides being equal length also make them congruent, which you can see in step 4:

Keep a Proof Reasons List
The postulates, theorems, properties, and definitions are likely all in your student’s textbook, but it can be easier to create a list or reference guide with your own notes to help you remember when to use them. Flashcards can also be helpful in learning these, according to this blog by Mrs. E.
If your student is still new to geometry and struggling to memorize all of these concepts, it can be useful to have them write out the concepts they are using in their reasoning when explaining a statement. This is another teaching tip and will help them, and you, see that they know what these postulates, theorems, properties, and definitions say, and – more importantly – that they know what they mean.
We know geometry can be some of the most difficult lessons to handle.
If your child needs extra geometry help and you don’t have the spare time, or the education, to help them master their geometry concepts, Thinkster will pair your child with an online math tutor who is an expert at geometry processes and is dedicated to making sure your child learns them properly.
Ready to help your child master geometry and other core math concepts, do better on an upcoming standardized test and improve their study skills? Your child can try Thinkster risk-free.
Thinkster provides a full-fledged platform (driven by AI, behavioral, and data science), as well as supplemental , help, , and more. Our Parent Insights App allows you to monitor your ‘s work and improvements at any time.
An elite, and system work together to help your go beyond just – we want them to master it.
Learn more about our curriculum and teaching style here.


