Thinkster Math: Tutoring Personalized by Patented AI + Top Math Tutors

Loading…

Angle Of Elevation And Depression | Trigonometry Math Help

Why is this concept useful?: This concept is very useful in real life because it can help find distances between objects and/or speeds of objects. Some examples include control/radar stations mapping the nearby planes, lighthouses watching over boats approaching the shore or someone just looking up at a cat in a tree.
Where does this concept fit into the curriculum?: High School Geometry

Related Topics

By Puja Varude

Math Tutoring to Boost Your Child’s Math Skills & Scores by 90% in Just 3 Months – Guaranteed!

Does your child struggle with math homework or understanding tricky math concepts? Do they do okay in math, but express excitement to learn new material or advanced math?

A Thinkster Math tutor provides one-to-one support to help elementary, middle school, and high school students build confidence and master math subjects like K-8 math, pre-algebra, algebra, geometry, calculus, and more.

Our expert math tutors customize math lessons to your child’s unique needs, making learning math fun and effective. We help students improve grades, develop strong critical thinking skills through solving word problems, excel in standardized tests, and develop strong problem-solving skills.

Our expert math tutors are ready to help make your child a champion and develop strong math mastery! Sign up for our 7-day free trial and get the best math tutor for your child today!

Start 7-Day Free Trial

What is an angle of elevation/depression?

Let’s say that you are looking at a plane flying in the sky. In this example, the angle of elevation would be the angle made between the object and the horizontal line made at your eye-level, like in the diagram below:

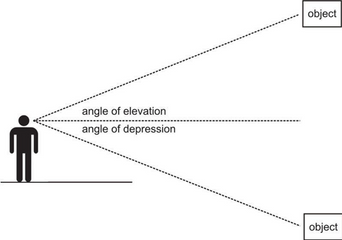
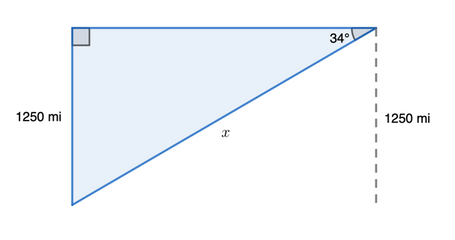
On the other hand, an angle of depression can be considered its reverse: if you were the pilot looking down at a person on land, then the angle of depression is the angle between the person on the land and the horizontal line at your eye-level, like in the diagram above.

How to use this concept?

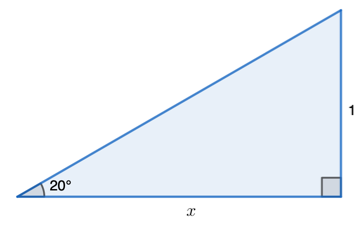
There are many ways one can use this concept. To begin, when an angle of elevation or depression is made, a right-angled triangle is also made, making concepts of trigonometry and Pythagorean theorem applicable. However, in angle of elevation and depression problems, trigonometry is more of a used concept since it includes angles.

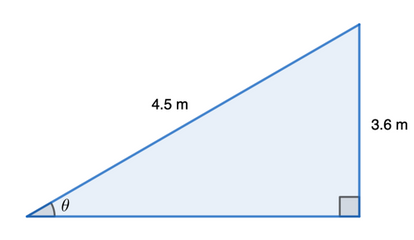
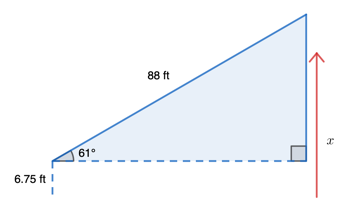
If we are given the angle of elevation or depression in a problem and one of the sides of the triangle, we can use trigonometry to find other sides or lengths of the given triangle. Sometimes, trigonometry and angle of elevation/depression can be an intermediate step to find other distances such as the distance of a bird in a tree or the distance between boats.

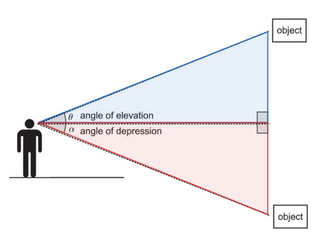
Equations pertaining the red and blue triangles both stem from trigonometry except the difference is that each triangle reference different sides and the angles are different,

\theta

and

\alpha

. However, the trig. equations hold in the same way. Below are a set of equations for the blue triangle with angle

\theta

sin\ \left(\theta\right)\ =\frac{opp}{hyp}\ \ \ \ \ \ cos\ \left(\theta\right)\ =\frac{adj}{hyp}\ \ \ \ \ \ \ \ tan\ \left(\theta\right)=\frac{opp}{adj}\

So, as you can see, knowing two of the variables, you can easily solve for another variable. Sometimes, you might be asked to find the angle of elevation/depression or a particular distance between two objects.

Sample Math Problems

Problem

Elon Musk just launched a rocket into the sky, and he is watching the take off several kilometers away from the launchpad. Given that the rocket has travelled 1 km from the launchpad (which is at Elon’s eye-level) and he knows the angle of elevation is 20°, how far away is he from the launch pad?

Solution

2.75 km. From the question, we can draw the following right-angled triangle to map the distances: