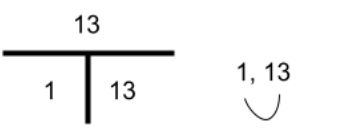Example: 2 3 5 7 ← prime numbers/factors
2 x 2 = 4
2 x 3 = 6 ← you can get to these numbers by
2 x 2 x 2 = 8 multiplying two prime factors/numbers
3 x 3 = 9 together
How can we use the concept:
There are two ways you can identify if a number is prime or composite:
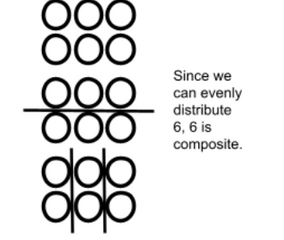
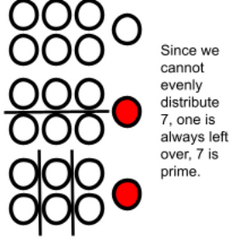
1. You can draw the number of dots for the number you are working with. You can then try to distribute them into even groups. If it can be distributed evenly among the groups, it will be composite. If it cannot, it will be prime. This concept can be used for lower grades who are not as familiar with factors and divisors; or students who are still working through their division facts. This method should be used sparingly, but would be a good way to introduce the topic to students.
Examples:
The number 6
b. The number 7
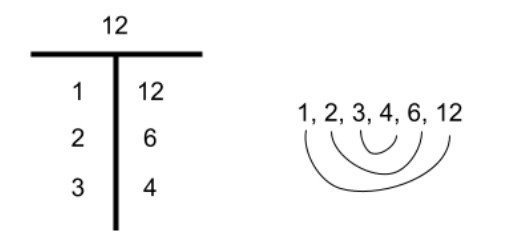
2. Identify the factors of the given number. If there are more than 2, or more than just 1 and itself, it will be composite. If it is just one and itself, it will be prime. This strategy is faster and more reliable.
Examples: a. The number 12
b. The number 13
Sample Math Problems
1. Is 25 prime or composite?
Solution:
25 is composite because there are three factors of 25. If there are more than two factors, the number is considered to be composite.
2. Which one of the following numbers is prime?
- 12 ← 1, 2, 3, 4, 6, 12 are the factors of 12. More than 2 factors = composite. 1 x 12 = 12, 2 x 6 = 12, 3x 4 = 12
- 13 ← 13 will be prime, because the only factors are 1 and 13 (itself). 1 x 13 = 13
- 14 ← 1, 2, 7, 14 are the factors of 14. More than 2 factors = composite. 1 x 14 = 14, 2 x 7 = 14
- 15 ← 1, 3, 5, 15 are the factors of 15. More than 2 factors = composite. 1 x 15 = 15, 3 x 5 = 15
3. Which one of the following numbers is composite?
a. 27 ← 1, 3, 9, 27 are the factors of 27. More than 2 factors = composite.
1 x 27 = 27, 3 x 9 = 27
b. 17 ← 17 will be prime, because the only factors are 1 and 17 (itself).
1 x 17 = 17
c. 31 ← 31 will be prime, because the only factors are 1 and 31 (itself).
1 x 31 = 31
d. 73 ← 73 will be prime, because the only factors are 1 and 73 (itself).
1 x 73 = 73
4. The number 30 is written as a product of its prime factors. What is the correct way of writing it?
Solution:
