What is Triangle Proportionality Theorem?
The Triangle Proportionality Theorem states that if a line parallel to one side of a triangle intersects the other two sides of the triangle, then the line divides the two sides proportionally.
How to Prove the Triangle Proportionality Theorem?
Let us consider a triangle △ABC
A line DE parallel to the side BC intersects the sides AB and AC.
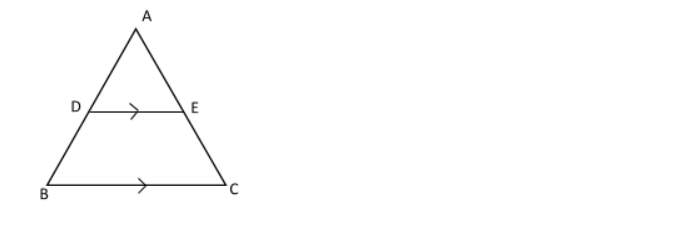
Thus, if DE // BC, prove that AD/DB = AE/EC
For the parallel lines DE and BC, the line AB is a transversal intersecting both lines.
The ∠ADE and ∠ABC are corresponding angles and thus congruent.
Similarly, for the parallel lines DE and BC, the line AC is a transversal intersecting both lines.
The ∠AED and ∠ACB are corresponding angles and thus congruent.
∠EAD is common to both △ABC and △ADE.
Therefore, △ABC is similar to △ADE.
Which means, AD/AB = AE/AC
AD/(AD + DB) = AE/(AE + EC)
AD (AE + EC) = AE (AD + DB)
AD(AE) + AD(EC) = AE(AD) + AE(DB)
AD(AE) + AD(EC) = AE(AD) + AE(DB)
AD(EC) = AE(DB)
AD/DB = AE/EC
Sample Math Problems
Question 1: In the figure given below, calculate the value of x.
Solution:
As DE // BC, as per the Triangle Proportionality Theorem,
AD/DB = AE/EC
5/7 = x/(x+6)
5 (x + 6) = 7x
5x + 30 = 7x
7x – 5x = 30
2x = 30
x = 15cm (Ans)
Question 2: In the figure given below, calculate the length of the side AC.
Solution:
As DE // BC, as per the Triangle Proportionality Theorem,
AD/DB = AE/EC
11/17 = x(x+36)
11 (x + 36) = 17x
11x + 396 = 17x
17x - 11x = 396
6x = 396
x = 66cm
Length of AC = AE + EC = x + x + 36 = 2x + 36 = 2 X 66 + 36 = 168 cm (Ans)
Question 3: In the figure given below, calculate the length of the side AC.
Solution:
As DE // BC, as per the Triangle Proportionality Theorem,
AD/DB = AE/EC
24/8 = x/19
x/8= 24 X 19/8 = 456/8
x = 57cm
Length of AC = AE + EC = x + 19 = 57+19 = 76cm (Ans)
Question 4: In the figure given below, calculate the value of x.
Solution:
As DE // BC, as per the Triangle Proportionality Theorem,
AD/DB = AE/EC
15/21= x/(x+4)
15 (x + 4) = 21x
15x + 60 = 21x
21x – 15x = 60
6x = 60
x = 10 cm (Ans)
