How can we use the concept:
When solving problems with square pyramids, we are most often looking for their surface area or volume.
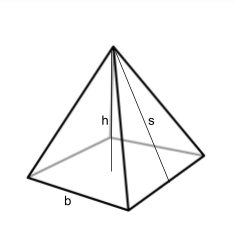
The surface area tells us how much area is needed to cover the outside of the pyramid. It can be found by adding the area of each face - the four triangles and the one square. Or you can use the formula which combines the area of all those sides for you:
Where s is the slant height and b is the side length of the square.
The volume tells us how much 3D space this pyramid fills. The formula for volume of a square pyramid is:
where b is the side length of the square and h is the height of the pyramid.
Sample Math Problems
Question
Find the surface area of the following pyramid:
Solution
The formula for surface area is SA = +2bs where s is the slant height and b is the side length of the square. In this case, s = 7 cm and b = 4 cm. By placing these numbers in the formula, we get:
