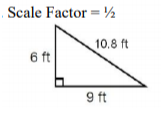
How can we use scale factor?
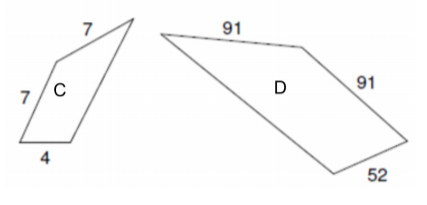
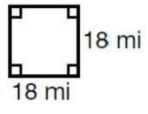
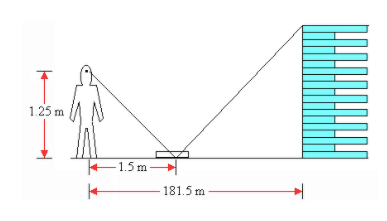
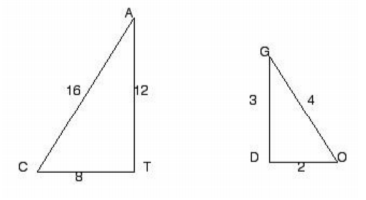
Scale factors help to visualize the large, real-world objects in a much smaller size. Typically, the larger measurement is the numerator and the smaller number is the denominator. If the scale factor is a whole number or the ratio is a fraction greater than 1, then the copy of it will be larger than the original. If the scale factor or ratio is a fraction between 0 and 1, then the copy will be smaller than the original. We can write scale factors as a ratio or as a fraction, just like ratios can!
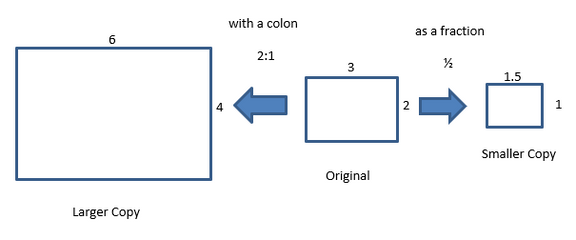
Visualize it through the following model:
The original copy is in the middle. See how when you have a scale factor of 2:1, the copy gets larger. However, when the scale factor is ½, you can see the copy gets smaller. Take a look at the measurements on the sides of the rectangle. You can see the larger one’s dimensions are double and the smaller one’s dimensions are exactly half.
If you are trying to determine the scale factor between two objects, you can use the following formulas.
To scale up, smaller to larger, you can use:
To scale down, larger to smaller, you can use:
Sample Math Problems
Question
The images below are similar figures. Find the scale factor from the image on the left to the image on the right.
Answer
Since we are finding the scale factor of the image on the left to the image on the right, we want a scale factor that will be greater than one. This is because the image on the right is larger than the one on the left. We will need to use measurements from the corresponding sides. In this case, we use the top of both figures.
