What happens when you look into a lake or a mirror? You see an image of yourself – a “reflection” of your real face but in the lake/mirror. This reflection is simply just a “flipped” version of the real object, which is your face. Similarly, in mathematics, you can also flip functions to get another function. This helps us understand about how we can manipulate a function to get another function.
How do you use this concept?
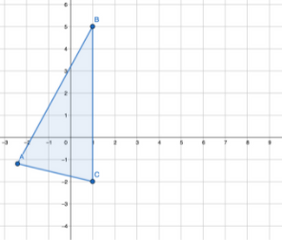
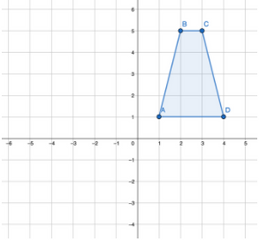
One of the first steps to understanding reflection is that any reflection of an object or a function has to be across a fixed line, which is often called the line of reflection. When you look at your reflection in the lake, the line (more so a plane) of reflection is the surface of the lake, somewhat like this picture:

Notice that in this picture, the size, shape, color is all the same as in the real world. The only change is that the image was flipped so the distance from the real object to the line of reflection is the same as from the image to the line of reflection. Previously, our line of reflection was the lake, but now we can change that to make the line of reflection a line on a x-y Cartesian plane (note the line of reflection can be any line in any direction – horizontal, vertical or even diagonal). We can reapply this concept in these three common scenarios - flipping across the x-axis, y-axis or the y = x line:
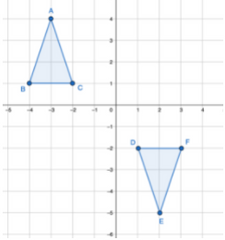
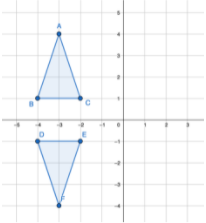
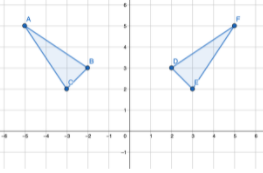
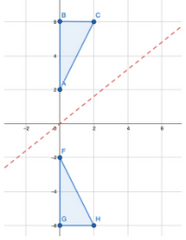
1. Flipping across the x-axis:
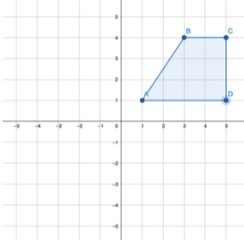
To flip across the x-axis, for all points of the real function/shape (x,y) we need to change it to (x,-y), like so:
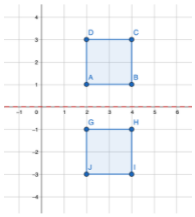
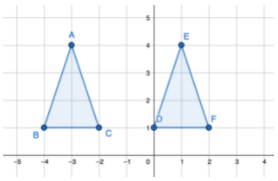
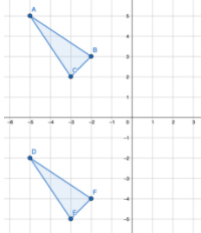
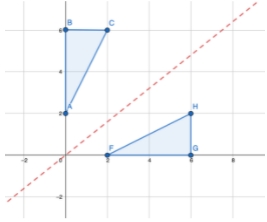
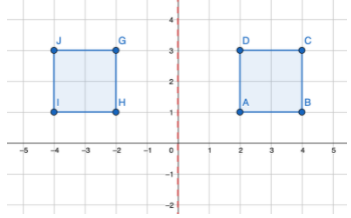
2. Flipping across the y-axis:
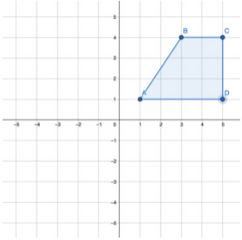
To flip across the y-axis, for all points of the real function/shape (x,y) we need to change it to (-x,y), like so:
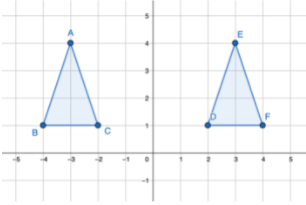
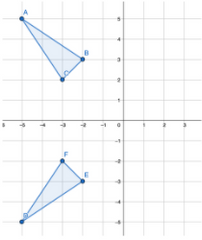
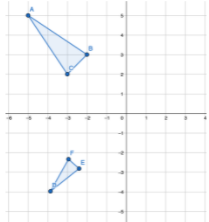
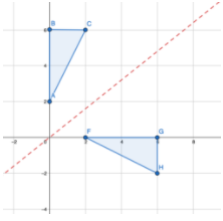
3. Flipping across the y = x line:
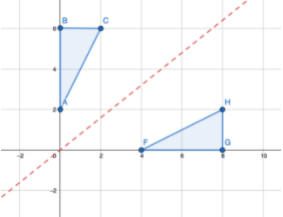
Recall that the y = x line is a diagonal line of the Cartesian plane that looks like:
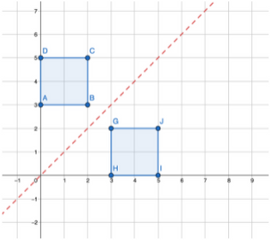
If you have a shape or line segment with co-ordinates, the process is similar to the previous two ways. For all points of the real function/shape (x,y) we need to change it to (y,x) (invert the co-ordinates).
Note that in any case of reflection, the distance between the real object and the line of reflection should be equal to the distance between the new (‘reflected’) image and the line of reflection. So, if co-ordinates are not provided, then you can simply just measure the distance, and draw a reflected image at the same distance away from the line of reflection.