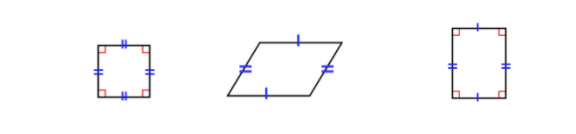
What are quadrilaterals?
To put it simply, a quadrilateral is defined as basically any 2-dimensional closed shape that has four sides (hence “quad”-rilaterals) and that is made up of only straight lines.
Due to the fact that a quadrilateral has only 4 sides, there are some important properties that you can use to solve for different quantities such as angles or lengths. Every quadrilateral has:
- Four edges/sides
- Four points/vertices
- Interior Angles (which sum to 360° in total)
As you are probably guessing, if only having 4 sides is the condition for a shape to be a quadrilateral, then there must be many different ways to draw them – you are right! Because there are different ways to draw them, there are some popular quadrilaterals. These types are drawn as below:
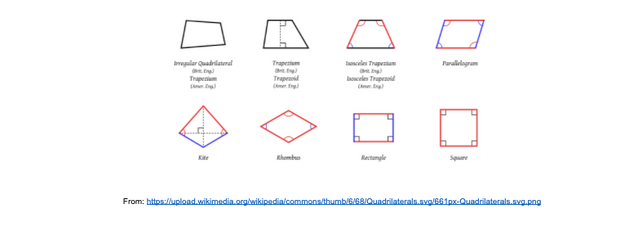
How to use this concept?
One can use the concept of quadrilaterals to find either lengths, angles (interior or exterior) and areas of quadrilaterals. Because of certain properties of different quadrilaterals, we can determine some of the missing lengths of sides of a quadrilateral or missing angles of a quadrilateral.
In another instance, we could use the concept in order to find the area of a quadrilateral. Now, as we mentioned previously, quadrilaterals can be drawn in all kinds of ways, therefore, there is no standard formula for all quadrilaterals. However, since we know there are some popular types of quadrilaterals, as covered previously, we can show the formulas for calculating these popular types:
Square:
In a square, the most important concept is that all sides are equal and all interior angles are the same – 90°. To find its area (A), we just need to multiply the length of one side (s) times itself:
A = (s)2
Rectangle:
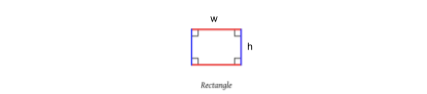
Similar to the square, here all the interior angles are the same – 90°, however, the opposite sides in this shape have the same length. So two of the sides are of equal length, and so are the two others. When it comes to find its area (A), we multiply the width (w) by the height (h) of the rectangle:
A = w • h
Parallelogram:
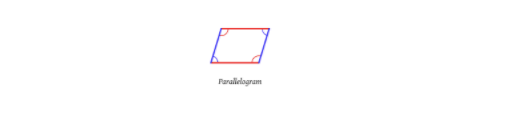
To find the area of a parallelogram, you need to know the height from the bottom base to the top and the length of the base or the top (length of the base and the top are the same in a parallelogram). The formula to find the area of a parallelogram is as below:
A = b • h
A = b • h
Rhombus/Kite:
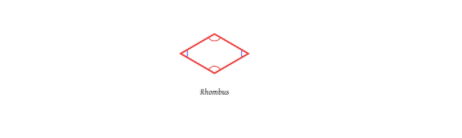
For the rhombus, the two most important dimensions that define the shape of a rhombus are the two diagonals. Note, a kite is just a type of rhombus, so the area to find a kite is the same way as you find it for a rhombus. To find the area, you need to multiply the lengths of the two diagonals and divide by two:
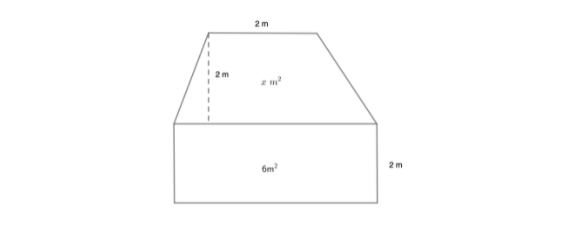
Trapezoid:
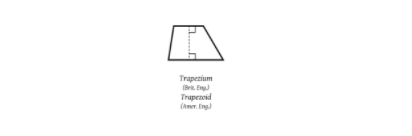
For the trapezoid, to find the area, you need add the two bases (top and bottom), divide by two and then multiple what you have with the height of the trapezoid:
Sample Math Problems
Question
For each of the shapes below, label which type of quadrilateral they are:
Answer
Shapes with the labels are as below:
Question
Given that you know that the two diagonals in a rhombus are 5cm and 8cm, then what is the area of the rhombus?
Answer
The area of a rhombus is calculated by multiplying the two diagonals and then dividing by two, so the answer to this problem is:
