What is Dilation?
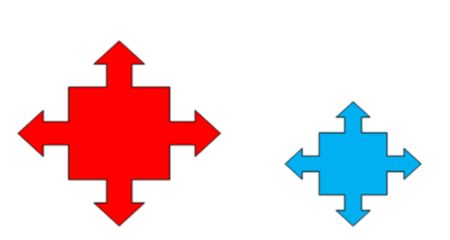
In geometry, a dilation is a transformation that changes the size of the original shape. When a dilation occurs, a figure will become enlarged or reduced, but will never change its original shape.

How to use dilation?
A dilation is a transformation that changes the size of a figure.
A scale factor is the measure of how large or how small an object becomes during the dilation.
If the scale factor is less than one, then the new figure will be reduced.
If the scale factor is greater than one, then the figure will be enlarged.
If the scale factor is equal to 1, then the two shapes are congruent.

Determining if a transformation is a dilation:

When an object is dilated, the shape never changes.

For example, in the image below, this is not a dilation because the triangle is enlarged, but the shape of the figure changed.

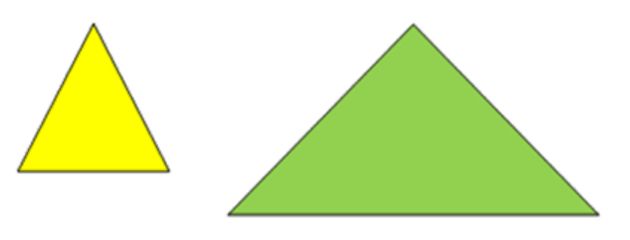
The next example is a dilation. Here the rectangle has been reduced and has kept the same shape.

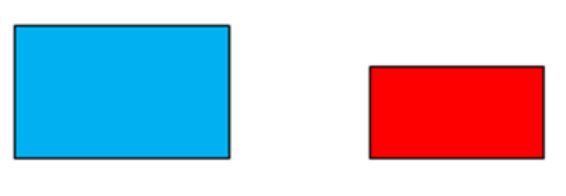
Finding the scale factor:

In order to find out how much an object has been dilated, we need to look at the scale factor.

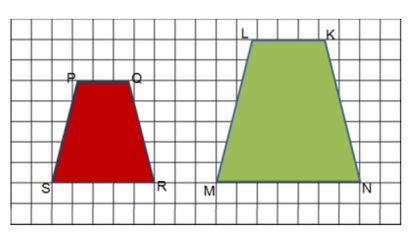
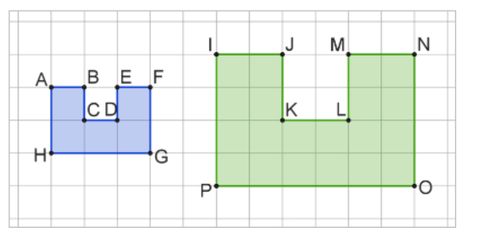
Example 1: To find the scale factor we first need to find the length of one side of the first shape

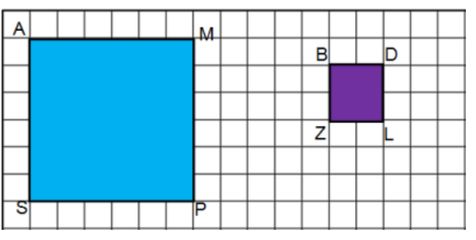
Solution:

In this case the side AS is 6 square units.

We then find the length of side BZ of the second shape. We use BZ because it is the corresponding side to AS.

BZ = 2 square units.

Now take the length of the second side and divide it by the first side.

Here you would divide the length of BZ by the length of AS.

BZ = 2

AS = 6

2 ÷ 6= 2/6. Simplified it is ⅓.

In this example the scale factor is ⅓. Since the scale factor is less than 1, the dilation resulted in the original image being reduced.

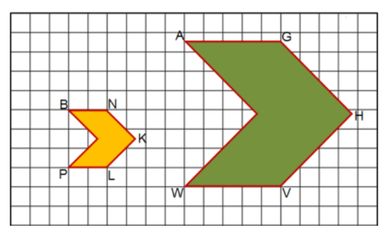
Example 2: In the next example, the dilation shows an enlargement of the original shape.

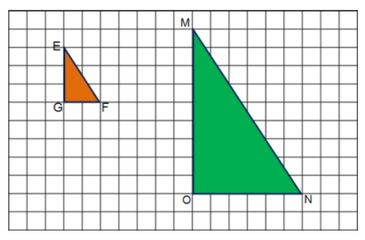
Solution:
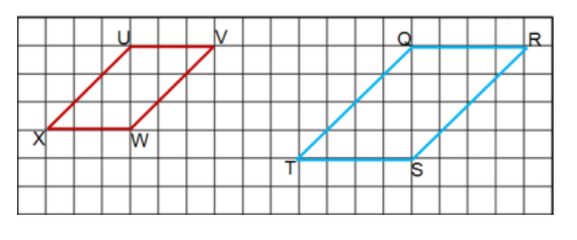
To find the scale factor for this example, we first need to find the length of one side of the first triangle.

In this case the side EG is 3 square units.

We then find the length of side MO of the second shape.

MO = 9 square units.

Now take the length of the second side and divide it by the first side.

Here you would divide the length of MO by the length of EG.

MO = 9

EG = 3

9 ÷ 3 = 3

In this example the scale factor is 3. Since the scale factor is greater than 1, the dilation resulted in the original image being enlarged.

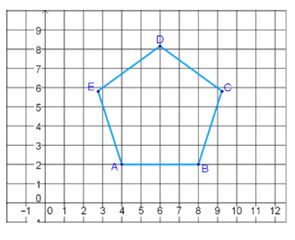
Finding the coordinates of the second image when dilated by a specific scale factor.

If given a figure and a scale factor, you can find the coordinates of the new shape by multiplying each number in the first figure’s coordinates by the scale factor. This will give you the new coordinates of the second figure.

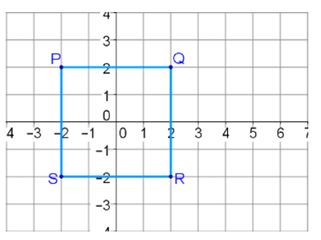
Example: The figure ABCD is dilated to form A’B’C’D’. The scale factor used is 4. What are the coordinates of point B’?

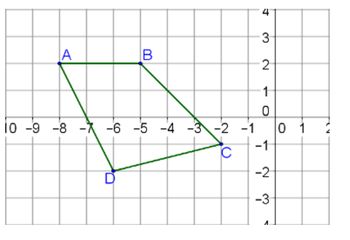
Here we see that the coordinates of B are (-5,2). To find the coordinates of B’, multiply each number in the coordinate pair by the scale factor 4.

B’=(-5x4,2x4)

B’=(-20,8)