How can we use conic sections?
Let’s begin with a visual of what the conic sections look like:
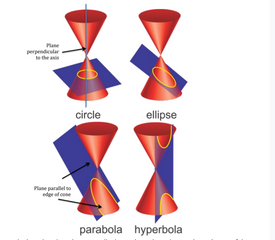
A circle is formed when the plane is perpendicular to the axis and goes through one of the cones.
An ellipse is formed when the plane intersects one of the cones but is not perpendicular to the axis.
A parabola is formed when the plane intersects one of the cones and is not perpendicular to the axis
A hyperbola is formed when a plane intersects both of the cones.
Depending on where the plane intersects the cone, it will change the size and shape of the conic section. All conic sections have the same general form:
Where A, B, C, D, E, and F are all real numbers.
The following will be a summary of each type of conic section.
1. Circles
A circle is the set of all points in a plane that are a distance r from a given point, called the center. The distance r is the radius of the circle.
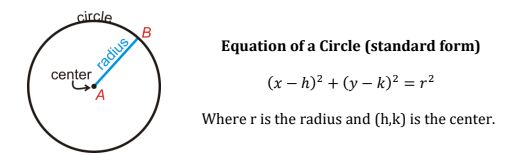
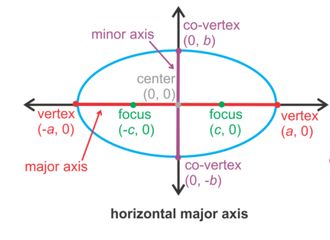
2. Ellipse
An ellipse is a set of all points (x, y) in a plane, the sum of whose distances from two fixed points called foci is constant.
The following are important values to be aware of for the ellipse.
C = Center (h, k)
F = Foci (two fixed points)
V = Vertices, found on the major axis
CoV = co-vertices, found on the minor axis
c = distance from the center to the foci
a = distance from the center to the vertices
b = distance from the center to covertices
e = Eccentricity of the ellipse, found by doing
(the closer to zero, the more of a circle shape, the closer to one the more elongated)
Major axis length = 2a
Minor axis length = 2b
The following image shows a horizontal ellipse, centered at the origin, whose major axis is horizontal and minor is vertical.
The equation for a horizontal ellipse in standard form is:
The following image shows a vertical ellipse, centered at the origin, whose major axis is vertical and minor is horizontal:
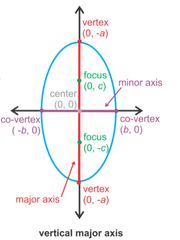
The equation for a vertical ellipse is:
Note that b and a switch places for either horizontal or vertical ellipses.
One other important thing to find would be c. The formula to find either a, b, or c looks like the Pythagorean theorem, but does have a difference in where the letters go. This formula can help find
3. Hyperbola
An ellipse is a set of all points (x, y) in a plane, the difference of whose distances from two fixed points called foci is constant. Pictured below:
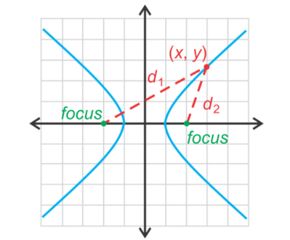
Hyperbolas have a a major and minor axis known as the transverse and conjugate axes respectively.
The following a horizontal hyperbola, centered at the origin, whose transverse axis is horizontal and conjugate is vertical
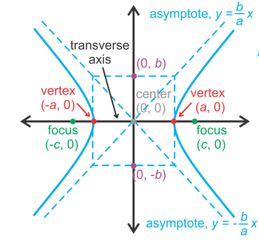
The standard form of a horizontal hyperbola is:
Note how the x and y switch places, not a and b like in an ellipse. Additionally, there is subtraction between the fractions.
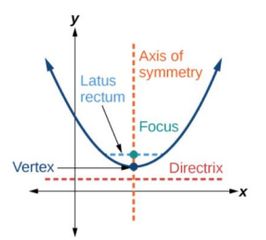
4. Parabola
A parabola can be defined differently than what you may be used to! We have this new line in, called the directrix, such that any point on the parabola is equidistant to the focus and the directrix. See the picture below!
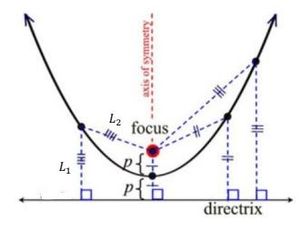
The standard form of a parabola takes on many forms to determine the direction in which it will open up.
has a vertex at (h,k) and will open upwards.
has a vertex at (h,k) and will open upwards.
has a vertex at (h,k) and will open to the right.
has a vertex at (h,k) and will open to the left. There also exists a segment, known as the latus rectum (L.R.) which goes through the focus and is perpendicular to the axis of symmetry and has endpoints on the parabola. The length of the L.R. is |4p| units where p is the distance from the vertex to the focus. See the picture below!
Sample Math Problems
1. Rewrite the following equation in standard form. State the center and radius of the circle.
