What is phase shifting?
As per the definition, a phase shift is the distance a function has horizontally moved from the original position of the function (usually (0,0) but the starting point may change based on the original function). This movement can be either left or right and the terminology of “phase shifting” is generally applied to trigonometric functions as they have phases. The generic counter-part term for all functions (such as algebraic or exponential) is just a horizontal shift.
How to use this concept?
One of the key ways to use the ideas of phase shift is to be able to determine the phase shift just from a graph so that we can get a better idea of how the graph changed. For example, from the graph below, we can tell that the function could look like a sinusoidal function, but it is horizontally moved to the right. It is important to note that when a graph is moved the left by x distance, then we add x from the inside of the function. However, if the graph is moved to the right, then we subtract.
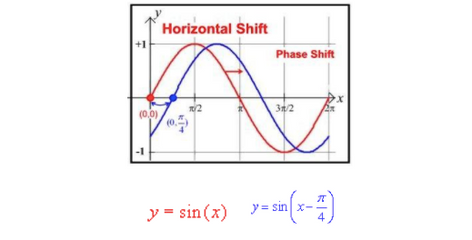
(redraw diagram and rewrite red and blue label with arrows)
Based on the above diagram, we see that the blue graph has moved to the left by so the phase shift is and in the equation for the blue function, we subtract the phase shift from x. If it were to be the opposite case of moving to the right, then the phase shift would be and we would add to x (essentially we are doing x -() = x + () because the original form of the equation is:
Note: A common mistake when finding the phase shift is not ensuring that the function is in the right form. The original form of sinusoidal function is:
Note how the coefficient of x is 1 and the B is factored out. Now, let us review a common mistake. Let’s say Tiffany says the phase shift is in y = sin sin( 2x - ). Unfortunately, Tiffany would be wrong because the equation is not in the original form. First we need to factor out the 2, to make the coefficient of x equal to 1, then we can say that the equation is:
KaTeX can only parse string typed expression
So the phase shift is actually
Sample Math Problems
Question
Consider the equation y = cos cos ( 3x-2 ) +2. What would be the phase shift?
Solution
First we would need to convert the equation to the standard form like so:
