What are rational expressions?
Rational expressions are fractions in which both the numerator and the denominator are polynomials.
How to simplify rational expressions:
A rational expression is simplified when the numerator and denominator no longer have a common factor.
To simplify rational expressions follow these steps:
- Factor both the numerator and the denominator.
- Reduce the fraction by canceling out any terms in the numerator and denominator that are the same.
- Rewrite the fraction with what is left over.
Let's look at an example:
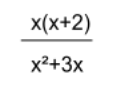
In this example, we first need to see if both the numerator and the denominator can be factored. The numerator is already factored, but the denominator is not.
To factor the denominator, we can factor an x out because both x²
and 3x have an x.
The denominator factored will be x(x+3)
Now we can write the rational expression as:
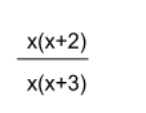
Next, we need to reduce the fraction by canceling out any terms in the numerator and denominator that are the same.
In this example the terms we can cancel out are the x’s that are found outside of the parenthesis.
Once we cancel out the x’s, the reduced fraction will be:
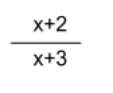
This can not be simplified any further, therefore it is the final answer.
Note: A common mistake is trying to cancel out the x’s in x+2 and x+3. These can not be cancelled out because they are part of the term The 2 and 3 do not have an x. Therefore, x can not be factored out.

















